Si seguim l’ordre que ens havíem proposat, ara tocaria parlar del quilogram. Del quilogram? Potser l’ordre més lògic hauria estat parlar ara de les unitats de temps, en tant que espai i temps són estretament lligats. Fins i tot, si ens atenem a les definicions del Sistema Internacional (les actuals i les predictibles en les properes dècades), hauria estat més assenyat començar pel “segon” i seguir després pel “metre” i pel “quilogram”. Al capdavall, en l’actualitat, el “metre” es defineix a través del “segon” mitjançant la constant universal de la “velocitat de la llum en el buit”. De forma anàloga, podríem esperar (no pas a curt termini) que el “quilogram” fos definit a través del “segon” mitjançant la constant universal de la “gravitació” (definida en termes newtonians o gaussians). Però, en l’actualitat el “quilogram” disposa d’una definició independent i, com veurem, un poc arbitrària. I del quilogram? No és el quilogram un múltiple del gram? No hauríem de parlar del gram? La relació històrica entre el quilogram i el gram és un xic més complexa que la que existeix entre el quilòmetre i el metre, com ja veurem. El Sistema Internacional, a més, es basa en el sistema M-K-S, que emprava com a unitats de referència el metre, el kilogram i el segon. El sistema M-K-S, més propi del laboratori universitari, s’imposà en aquest sentit al sistema c-g-s (centímetre – gram – segon) que empraven els enginyers. Ens tocarà en aquest capítol veure la relació entre un i l’altre. Començarem, però, per parlar de les unitats de massa tradicionals. Unes unitats que, originàriament, són unes “unitats de pes”.
El pes de les coses
La història del desenvolupament de les unitats de longitud va lligada a l’agrimensura (els camps es mesuren en unitats de superfície, és a dir de longitud x amplada), o a la compra-venda d’objectes definits per la longitud (des de serveis de transport, a cordills i cordes, fils, teles, etc.). No obstant això, si hi ha una magnitud física que pren protagonisme en els intercanvis de mercaderies és el “pes”.
A mesura que els metalls nobles guanyen paper com a mitjà d’intercanvi universal (i com a mitjà d’atresorament, i com a mitjà de pagament), el preu de les coses començarà a expressar-se en unitats de pes d’or o d’argent. Així doncs, com veurem tot seguit, la unitat de pes tradicional per excel•lència, la lliura, també serà, en forma de “lliura d’or” la unitat de moneda per excel•lència. La equivalència en “lliures d’or” de tantes lliures de mercaderia informa de la densitat de valor d’aquesta mercaderia. El valor de les coses destinades al mercat, és clar, continua associat al temps social de treball necessari per a produir-les. I també aquest és el valor associat a l’or i a l’argent. Però la pròpia universalitat adquirida pels metalls nobles els farà identificats amb el valor.
Les unitats de pes
Òbviament, tot això conduirà al desenvolupament de tècniques de “pesada”. La feina d’estandardització de les pesades, de la vigilància contra fraus, etc., és ben antiga. Serà un motor de la institucionalització dels intercanvis, de la fixació de les monedes, etc. No és estrany que el símbol de la justícia sigui una balança, o que una balança fos l’instrument que, d’acord amb la religió egípcia, decidia el destí de l’ànima a través de la pesada del cor del difunt en relació amb una ploma.
Abans de Galileu i de Newton, pes i massa són la mateixa cosa. La humanitat, fet i fet, viu en una fina capa superficial d’un planeta concret. L’acceleració gravitatòria, a tots els efectes pràctics, és uniforme. El valor de la g es pot prendre com una constant, i pes i massa són idèntics. El pes és, però, la força amb la qual una massa és atreta gravitatòriament sota el camp gravitatori g (P = mg•g). Una relació que és idèntica a la de qualsevol força en general (F = mi•a). La identificació entre la massa gravitatòria (mg) i la massa inercial (mi) és a la base de la teoria universal de la relativitat.
Però no ens avancem gaire en el nostre relat. En tot cas, reiterem la identificació històrica entre “unitats de pes” i “unitats de massa”. O, si ho volem, direm que la massa dels objectes és determinada (i definida) pel pes.
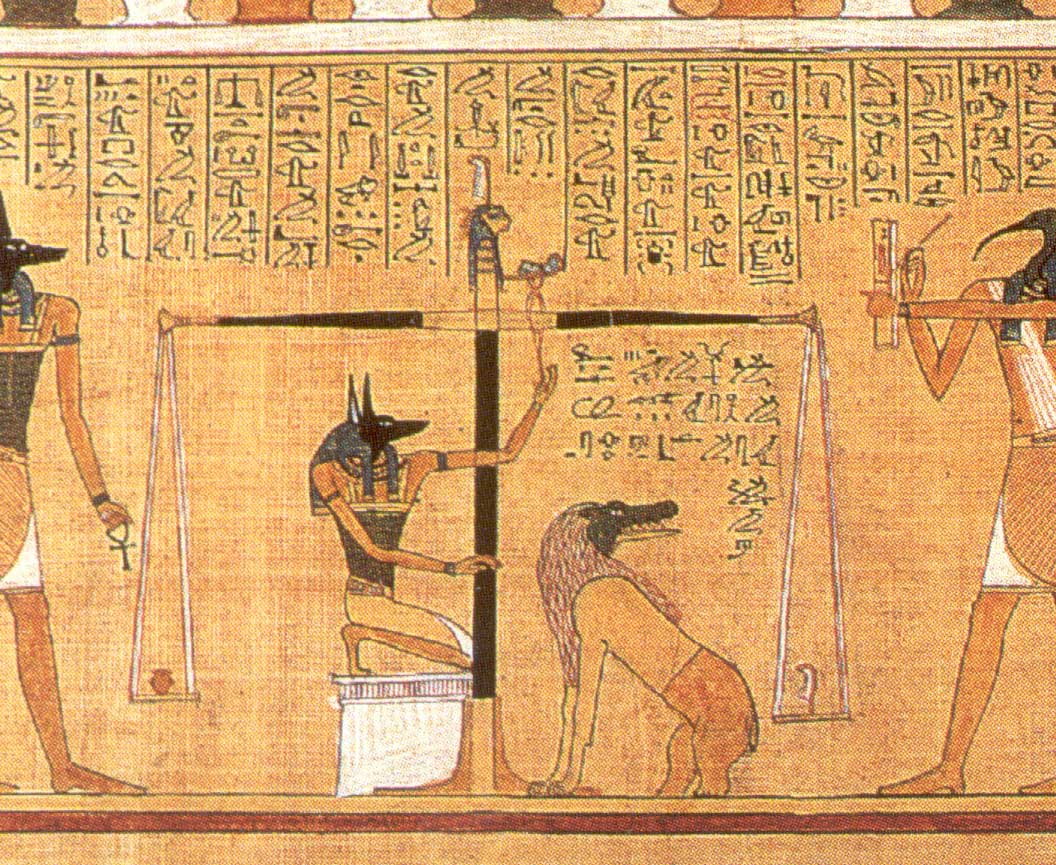
Aquest papir del segle XIII a.C., ens mostra la pesada del cor d’un difunt. Anubis s’encarrega de fer servir la balança. El pes és comparat, qualitativament, amb una ploma. El cor de la imatge és més lleuger que la ploma, indici de la noblesa, que serà guardonat amb una vida d’ultratomba plena de joia.
En parlar de les unitats de longitud o de distància ens trobavem amb la possibilitat de la comparació directa. Hom podia apamar un objecte, o comptar les passes d’un terreny. Si de cas volia més precisió podia fer mà de vares o de canes degudament homologades. Però, i el pes? Sopesar dues coses, una a la mà dreta i una a la mà esquerra no és gaire precís. Generalment la mà directora també és la mà més forta, i caldrà que la diferència sigui clara per poder detectar-la. L’origen de les balances, doncs, es perd en la nit del temps. Inicialment, les balances, basades en el principi de la palanca, servien per comparar els pesos de dos objectes (o de dues quantitats). Hom pesava, a banda i banda, quantitats de la mateixa substància, i així es podien fer repartiments justos. La transició cap a l’ús d’un equivalent més o menys universal, és a dir, fonamentalment, un material no-perible i gravimètricament dens, faria que les balances sempre tinguessin a una banda aquest equivalent. Si, en una balança, fem servir sempre en un dels braços un o més objectes similars, ja passem de mesurar un “pes relatiu” a mesurar un “pes absolut” expressat en unitats definides per aquestes peses.
A la vall de l’Indus, fa uns 4000 anys, hom emprava com a peses pedres polides de forma cúbica. Les pedres podien provindre de roques diferents, i tant se valia el volum de la pedra. El que importava era que les pedres s’ajustessin a 1 unitat de pes, a 2 unitats, a 3 unitats, etc. També a Egipte trobem peses similars. Les marques en aquestes peses permeten deduir que les pedres volien representar equivalents d’or. És possible que les pedres haguessin substituït l’or en la funció de patró.
Al llarg dels mil•lennis següents, les peses seran cada vegada més sofisticades quant a forma, garantia de la fiabilitat del pes. Hi haurà una normalització creixent de les unitats. Això contrasta amb la lenta evolució de la pròpia balança. Les primeres balances de torsió no arriben fins als segles XVII o XVIII a Europa. Cal esperar al segle XIX per trobar-les en forma de balances de precisió, utilitzades en el laboratori de química, o en les oficines postals. Les balances electròniques apareixen en les darreres dècades del segle XX.
Vegem, però, algunes de les unitats de pes tradicionals a casa nostra:
– la lliura. La lliura és la unitat de pes per excel•lència, tal com hem dit. Etimològicament es vincula a les peses emprades en la balança tradicional. Se suposa que és una unitat que es defineix com el pes màxim que hom pot resistir amb comoditat sostingut amb una sola mà. La lliura variava de país a país, de ciutat a ciutat, de ram a ram. Per exemple, els apotecaris feien servir una lliura relativament lleugera. Entre els carnissers es feia servir una lliura grossa que valia per tres lliures d’altres rams (o, dit d’una altra manera, una lliura carnissera equival a tres terces). Així doncs, tenim dues línies de definició: la lliura habitual o lliura tendera, i la lliura grossa que fa entre el doble i el triple de la primera. La lliura també s’utilitzava per mesurar líquids, si bé, els líquids eren sovint definits no en relació al seu pes sinó en relació al seu volum: per això la lliura també és una mesura de capacitat per a recipients. La lliura d’or era la base del sistema monetari. Òbviament és una unitat prou gran i, lògicament, la lliura se subdividia en subunitats: 15 reals (1 real és un quinzet de lliura), 20 sous o morabatins. Com que la terra també és subjecte de compra-venda, no és estrany que la lliura (d’or) també esdevingués una unitat de superfície agrària (per exemple, 1 lliura = 40 quarteres).
– l’unça. Per a moltes transaccions, una lliura és una unitat massa gran. Progressivament, les lliures d’alguns rams van perdre pes, tal com passà amb la lliura d’or. Una altra alternativa és dividir la lliura en dotze parts, cadascuna de les quals és una unça. Com la lliura, l’unça també és una unitat monetària, en aquest cas encarnada en monedes d’or de valor considerable (1 unça = 16 duros).
– el marc. Situat entre l’unça i la lliura, hi ha el marc. El marc s’adaptà al sistema per esdevindre equivalent a 8 unces (i, per tant, a 8/12, o 2/3, de lliura). El marc s’utilitzà sobretot com a unitat monetària i, al llarg de la història, les seves equivalències en lliures i onces d’or o d’argent van canviar. El mot ‘marc’ és un germanisme, com ‘marca’ (el verb ‘marcare’ no existí en llatí clàssic), i pot semblar irònic que els darrers ‘marcs’ en circulació hagin estat els de la República Federal d’Alemanya.
– l’arrova. L’arrova és un múltiple de la lliura. Quin múltiple exacte, però, varia segons el gènere que es pesava o segons la localitat. Trobem arroves de 24 lliures, però també de 26, 27, 30, 32, 33, 34, 35 o 36 lliures. L’arrova, igualment, també pot ésser un múltiple de la lliura com a unitat de volum (‘arroves d’oli’). El nom d’arrova és d’origen llatí, i vol dir literalment, “quarta”.
– el quintar. De quina unitat és ‘quarta’, l’arrova? La resposta més general ens condueix a una altra fracció, el quintar. Fet i fet, però, el quintar es defineix com el pes equivalent a quatre arroves, i per això l’equivalència en lliures és variables, si bé volta les 120 lliures. Però, és el quintar la cinquena part d’una altra unitat? Des d’un punt de mira etimològic no és el cas. El mot ‘quintar’ prové de l’àrab, ‘qintar’, que vol dir ‘centenar’ i fa referència al fet que el quintar fa unes 100 lliures.
– la tona: la tona es feia servir més habitualment com a unitat de capacitat per a grans volum. Etimològicament prové del celta, tunna, que vol dir pell, i fa referència a la pell amb la qual es fan les bótes de vi. La tona es podia subdividir en ‘sesters’. No és sinó tardanament, que hom voldrà convertir la tona en una unitat de massa general per a mercaderies, entesa com a múltiple de ‘quintars’.
– el pes. La paraula germànica per designar la ‘lliura’ és el pfund/pound. La paraula ‘pes’ també es feia servir per designar la unitat de pesada de determinats rams.
– la mesura. El mot ‘mesura’ també apareix per designar una altra unitat, però no tant de pes, com de volum. Els líquids, en general, però també els sòlids de gra fi, són més fàcils de definir en termes de volum que no pas de massa. Els recipients de ‘mesura’ definien tota una sèrie d’unitats de volum: barralons, porrons, etc., que tenien també la conversió indirecta en unitats de massa.
La llista no és pas exhaustiva, però mostra la diversitat d’unitats i la multiplicitat de definicions. No n’hi havia prou amb parlar de ‘lliures’ o d’‘arroves’, sinó que calia definir ben clar de quin ram i de quina localitat i, sota el control de quina autoritat, anava l’encàrrec de vigilar peses i balances.
En el proper subcapítol veurem com els antecedents del sistema mètric van presentar la qüestió d’estandarditzar unes unitats de massa (i, per extensió, de pes i de volum).